在下边的学习中，主要是学习指定一个点（源点）到其余的各个顶点的最短路径，也叫做“单源最短路径”。

例如下图中的1号顶点到2，3，4，5，6顶点的最短路径：

在这里要和flody算法一样，在这儿也需要用二维数组e来存取顶点之间和边之间的关系，数值如下：

在这儿我们还需要用一个一维数组dis来存取1号顶点到各个顶点的初始路程，如下：

因为dis中存取的是各个顶点到1号顶点的初始距离，所以我们把dis数组中的值称为最短路的“估计值”。

既然我们是求1号顶点到其余各个顶点的最短路程，那我们就可以先找一个距离1号顶点比较近的顶点。

我们通过看dis数组可知距离1号最近的是2号顶点。当我们选择了2号顶点之后，dis[2] 中的值由一个“估计值”变成了一个“确定值”，即1号顶点到2号顶点的最短路程就变成了当前的dis[2]的值。

当我们选定了2号顶点，我们接下来看2号顶点有哪些出边，有2-->3和2-->4这两条边，我们可以通过讨论2-->3这条边是否让1号到3号顶点的路程，也就是说现在我们来比较dis[3] 和 dis[2] + e[2][3] 的大小，其中dis[3] 表示1号顶点到3号顶点的路程：dis[2]
+e[2][3]中dis[2]表示1号顶点到2号顶点的路程， e[2][3]表示2-->3这条边。所以dis[2] + dis[2][3] 就表示从1号顶点到2号顶点，再通过2-->3这条边，到达3号顶点的路程。

dis[3] = 12 , dis[2] + e[2][3] = 1 + 9 = 10   ，dis[3] > dis[2] + e[2][3] ,因此dis[3] 要更新为10，这个过程我们成为“松弛”，1号顶点到3号顶点的路程即dis[3] , 通过2-->3这条边松弛成功。

这就是dijkstra的主要思想：通过“边”来松弛1号顶点到其余各个顶点的路程。

   同理，我们可以通过2-->4(e[2][4]),我们可以将dis[4]的值从∞ 松弛为4（dis[4]初始为∞，dis[2] + e[2][4] = 1 + 3 = 4 , dis[4] > dis[2] + e[2][4] , 因此dis[4]的更新为4）

   我们对2号顶点松弛之后的dis数组为：

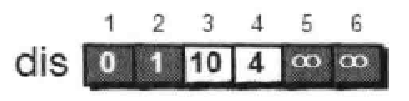
我们对4号顶点的所有边(4 -- > 3 , 4 --> 5 和 4-->6)还用刚才的方法进行松弛，松弛之后为：

接下来对3号顶点的所有出边（3-->5)进行松弛，松弛之后的dis数组为：

对5号顶点的所有出边(5 --> 4）进行松弛，松弛完毕的dis数组为：

最后对6号顶点的所有出边进行松弛，得到最终的dis数组，这就是1号到所有点的最短路径：

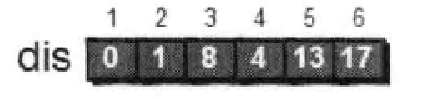
         我们来对上边的算法来进行一个总结，上述的算法的思想是：每次找到离源点（上述例子的源点就是1号顶点）最近的一个点，然后以该顶点为中心进行扩展，最终得到源点到其他点的最短路径。

完整的dijkstra的算法代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 1009;
int e[MAXN][MAXN];

int main()
{
    int dis[MAXN] , book[MAXN] ;
    int n , m , t1 , t2 , t3 , u , v , mi;
    while(cin >> n >> m)   //n代表点的个数，m代表边的条数
    {
        for(int i = 1 ; i <= n ; i ++)   //初始化
        {
            for(int j = 1 ; j<= n ; j ++)
            {
                if(i == j)
                    e[i][j] = 0;
                else
                    e[i][j] = INF;
            }
        }

        for(int i = 1 ; i <= m ; i ++)
        {
            cin >> t1 >> t2 >> t3;
            e[t1][t2] = t3;
        }

        for(int i = 1 ; i <= n ; i ++) //初始化dis数组，这里是1号到其余各个顶点的初始路程
        {
            dis[i] = e[1][i];
        }

        //book 数组的初始化
        for(int i = 1 ; i <= n ; i ++)
            book[i] = 0;
        book[1] = 0;

        //dijkstra算法的核心语句
        for(int i = 1 ; i <= n ; i ++)
        {
            //找到距离1号顶点最近的点
            mi = INF;
            for(int j = 1 ; j <= n ; j ++)
            {
                if(book[j] == 0 && dis[j] < mi)
                {
                    mi = dis[j];
                    u = j;
                }
            }
            book[u] = 1;
            for(int v = 1 ; v <= n ; v ++)
            {
                if(e[u][v] < INF)
                {
                    if(dis[v] > dis[u] + e[u][v])
                        dis[v] = dis[u] + e[u][v];
                }
            }
        }
        //输出最终的结果
        for(int i = 1 ; i <= n ; i ++)
        {
            cout<<dis[i]<<" ";
        }
    }
    return 0 ;
}
/*
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4


0 1 8 4 13 17
*/

通过上述代码可以看出来，这个算法的时间复杂度是O(N²)。其中每一次找到离1号顶点最近的点的时间复杂度是O（N），我们可以对这一算法进行优化，使这一部分的时间复杂度降低到O（logN）。

另外对于边数M少于N²的稀疏图来说（我们把M远小于N²的图称为稀疏图，而M相对较大的图我们称为稠密图），我们可以用邻接表来代替邻接矩阵，使得整个代码时间复杂度优化到O(M+N)log N 。 这种情况下最坏的情况就是M就是N²，这样的话（M+N）log N要比N²还要大，但是大多数情况下并不会有这么条边。。因此（M+N）log N要比N²小的多。

我们来说一下如何用邻接表来存图，我们可以先看数据：

4 5
1 4 9
2 4 6
1 2 5
4 3 8
1 3 7

第一行的两个数是n，m。n表示顶点的个数（顶点编号为1~n），m表示边的条数。

接下来的m行，每行都有三个整个t1，t2，t3.表示顶点t1到顶点t2的权值为t3。

我们用邻接表来存储这个图，代码如下：

int n , m ;
int u[1009] , v[1009] , w[1009];
int first[1005] , next[1005];
cin>>n>>m;
//初始化first数组下标1~n的值为-1，表示1~n顶点暂时都没有边
for(int i = 1 ; i <= n ; i ++)
{
    first[i] = -1;
}
for(int i = 1 ; i <= m ; i ++)
{
    cin >> u[i] >> v[i] >> w[i];  //输入每一条边
    next[i] = first[u[i]];//关键语句
    first[u[i]] = i ;
}

在这里说的是使用该数组来实现邻接表，没有真正使用指针链表，这是一种在实际应用中非常容易实现的方法，这种方法为每个顶点 i（i从1~n）都设置一个链表，里面保存了从顶点 i 出发的所有的边（这里用first 和 next 数组来实现）

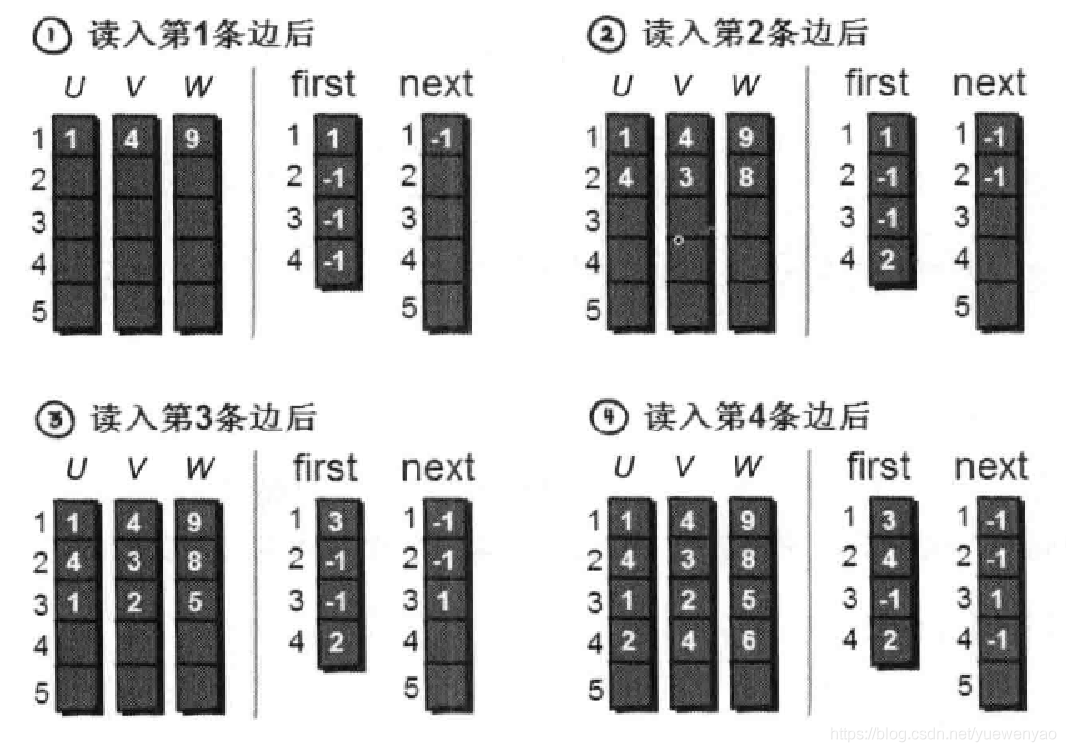
首先我们需要为每一条边进行1~m的编号。用u，v和w 三个数组来记录你每条边的信息，即u[i] , v[i] 和 w[i]表示的是第 i 条边是从u[i] 号顶点到v[i] 号顶点(u[i] --> v[i])，且权值为w[i]。

first 数组的1 ~ n号元素单元格分别用来存储 1 ~ n 号顶点的第一条边的编号，初始的时候因为没有边加入，所以都是-1。即first[u[i]] 保存顶点u[i]的第一条边的编号，next[i] 存储的是 ”编号是i的边“ 的” 下一条边“的编号。

接下来我们看一下存入一条边之后的每一个数组的元素的值。

接下来我们要考虑的就是我们应该怎么遍历每一条边。

上边说的其实first数组存的是每个顶点 i （i 从1~n）的第一条边。比如1号顶点的第一条边是编号为5的边（1，5，7），2号顶点的第一条边是编号为 4 的边（2，4，6） ， 3 号顶点没有出向边， 4 号顶点的第一条边的编号为2的边（2 4 6），那么我们如何遍历1号顶点的每一条边呢？看下图：

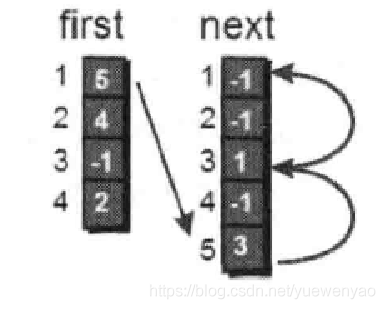
在找到1号顶点的第一条边后，剩下的边都可在next数组中依次找到。看代码：

k =  first[1];
while(k != -1)
{
    cout<<u[k]<<v[k]<<w[k]<<endl;
    k = next[k];
}

我们仔细看可以发现遍历某个顶点的边的时候的遍历顺序正好与读入时候的顺序相反。

因为我们在为每一个顶点插入边的时候都是直接插入“链表” 的首部，而不是尾部。不过这样并不会有什么问题，这正是这种方法的奇妙之处。我们来遍历每个顶点的边，其代码如下：

for(int i = 1 ; i <= n ; i ++)
{
    k = first[i];
    while(k != -1)
    {
        cout<< u[k] << v[k] << w[k] << endl;
        k = next[k];
    }
}

我们可以发现使用邻接表来存储图的时间空间复杂度是O（M），遍历每一条边的时间复杂度也是O（M）。如果是稀疏图的话，M要远小于N²。因此稀疏图选用邻接表来存储要比用临界矩阵存储好的多。